Обобщающий урок по теме "Уравнения с параметрами" . 7класс.
![]()
«Решение уравнений с параметрами»
7 класс
Солдатова Светлана Анатольевна
учитель математики первой категории
МОУ Угличский физико-математический лицей
2017 год
Цели и задачи:
-
Образовательная: повторить, обобщить и систематизировать знания, умения и навыки необходимые при решении линейных уравнений с параметрами с применением алгоритма.
-
Воспитательная: воспитывать интерес к алгебре, применяя интересные задания; формирование личностных качеств: сосредоточенность и внимание; настойчивость и ответственность
-
Развивающая: развивать познавательные интересы в процессе решения нестандартных задач, умения владеть математической терминологией, правильно и четко выражать мысль.
Ход урока:
 .
Организационный момент.
.
Организационный момент.
-Сегодня на уроке мы будем работать над темой «Уравнения с параметрами», а именно над решением линейных уравнений с параметрами. Наша задача: хорошо отработать алгоритм решения и применять его при выполнении разнообразных заданий.
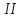 .
Устный упражнения:
.
Устный упражнения:
–Несколько устных упражнений окажут вам помощь при решении уравнений с параметрами, напомнят их суть и способ решения.
а) При каком условии имеет смысл выражение:
1)
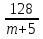 (
(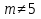 )
)
2)
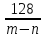 (
( )
)
3)
 (
(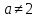 )
)
- Почему при данных значениях переменных выражение не имеет смысла?
(знаменатель обращается в нуль, а на нуль делить нельзя)
б) Решить уравнения:
1)
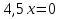 (
( )
)
2)
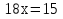 (
(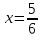 )
)
3)
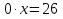 (
(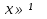 )
)
4)
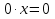 (
(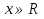 )
)
в) Найти множество корней уравнения:
1)
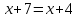 (
(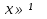 )
)
2)
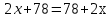 (
(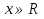 )
)
3)
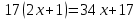 (
(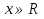 )
)
Как можно назвать два последних равенства?
Какое равенство называется тождеством?
г)
Укажите
множество значений переменной
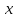 ,
при которых обращается в истинное
высказывание следующее предложение:
,
при которых обращается в истинное
высказывание следующее предложение:
1)
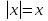 (
(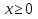 )
)
2)
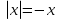 (
(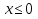 )(
)(
 Решение линейных
уравнений с параметрами.
Решение линейных
уравнений с параметрами.
а) Повторение алгоритма решения
– Что значит решить уравнение с параметром? (для каждого значения параметра указать множество решений уравнения)
– Какой
вид имеет линейное уравнение? (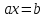 )
)
– Что
является решением данного уравнения
относительно
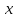 с параметрами
с параметрами
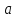 и
и
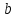 ?
?
если
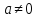 ,
то
,
то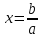
если
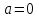 ,
,
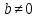 ,
то
,
то
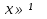
если
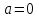 ,
,
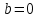 ,
то
,
то
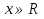
- Вышесказанное можно оформить в виде таблицы, которая представляет алгоритм решения линейных уравнений с параметрами.
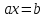
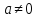
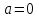 ,
,
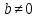
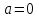 ,
,
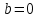
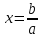
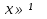
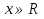
б) Решить уравнения (устно):
1)
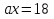
2)
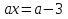
3)
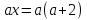 .
.
в) Сравнение решения уравнений:
1)
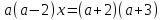 .
.
Решение:
Если
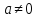 и
и
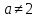 ,
то можно выполнить деление обеих частей
уравнения на коэффициент при
,
то можно выполнить деление обеих частей
уравнения на коэффициент при
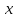 ,
т.е.
,
т.е.
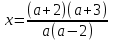 ;
если
;
если
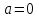 ,
то уравнение принимает вид
,
то уравнение принимает вид
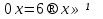 ; если
; если
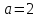 ,
то уравнение принимает вид
,
то уравнение принимает вид
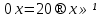 ..
..
Ответ:
при
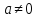 и
и
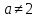
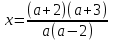 ,
,
при
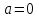 или
или
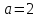
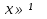 .
.
2)
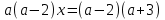
Решение:
Если
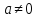 и
и
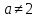 ,
то можно выполнить деление обеих частей
уравнения на коэффициент при
,
то можно выполнить деление обеих частей
уравнения на коэффициент при
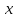 ,
т.е.
,
т.е.
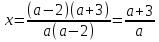 ;
если
;
если
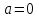 ,
то уравнение принимает вид
,
то уравнение принимает вид
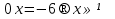 ; если
; если
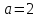 ,
то уравнение принимает вид
,
то уравнение принимает вид
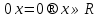
Ответ:
при
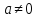 и
и
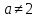
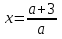 ,
,
при
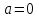
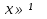 .
.
при
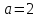
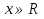 .
.
-В
обоих уравнениях при
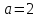
 коэффициент
при
коэффициент
при
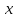 обращается
в нуль. Почему в первом случае уравнение
не имеет решений, а во втором случае
имеет бесконечное множество решений?
(В первом уравнении при
обращается
в нуль. Почему в первом случае уравнение
не имеет решений, а во втором случае
имеет бесконечное множество решений?
(В первом уравнении при
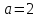 левая часть равна нулю, а правая отлична
от нуля, а во втором уравнении при
левая часть равна нулю, а правая отлична
от нуля, а во втором уравнении при
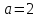 левая и правая части равны нулю при
любом
левая и правая части равны нулю при
любом
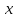 )
)
г)
Решение уравнений, требующих предварительных
преобразований для приведения их к виду
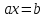 .
.
1)
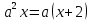
Решение:
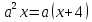
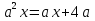
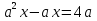
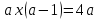
Если
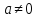 и
и
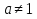 ,
то
,
то
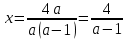 ;
;
если
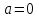
 ,
то
,
то
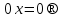
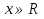 ;
;
если
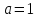
 ,
то
,
то
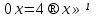 .
.
Ответ:
при
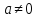 и
и
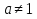
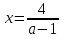 ;
;
при
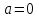
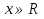
при
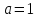
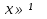
2)
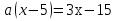
Решение:
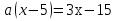
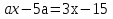
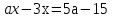
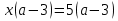
Если
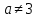 ,
то
,
то
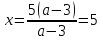 ;
;
если
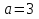
 ,
то
,
то
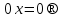
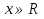 ;
;
Ответ:
при
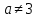
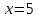 ;
;
при
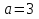
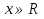
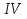 .
Cамостоятельная
работа.
.
Cамостоятельная
работа.
1
вариант:
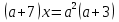
2
вариант:
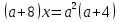
(2 человека работают за доской с последующей проверкой)
 .
Рефлексия.
.
Рефлексия.
Из перечисленных ниже уравнений выбрать те, в которых
а)
каждому значению параметра
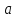 соответствует единственное значение
параметра
соответствует единственное значение
параметра
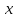 ;
(1, 4)
;
(1, 4)
б) при любом значении параметра уравнение не имеет корней; (2, 7)
в)
уравнение не имеет корней при
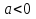 ;
(5, 8)
;
(5, 8)
г) при каком-то одном значении параметра было корнем любое действительное число, а при остальных значениях параметра решений не было. (3, 6)
1)
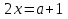 ;
;
2)
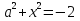 ;
;
3)
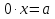 ;
;
4)
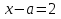 ;
;
5)
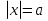 ;
;
6)
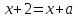 ;
;
7)
 ;
;
8)
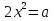 .
.
 .
Подведение итогов.
.
Подведение итогов.
 Домашнее задание.
Домашнее задание.
Решить уравнения с параметрами:
1)
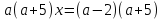
2)
 .
.
- Вебинар «Социализация и социальные навыки дошкольников: учимся общаться, договариваться, взаимодействовать»
- Современные тенденции развития шахматного образования в РФ. Научные идеи и концепции обучения шахматной игре
- Вебинар «Нейропсихологические методы диагностики и коррекции нарушений в развитии гиперактивных детей»
- Международный вебинар «Нейропсихологический подход в проектировании коррекционных курсов для индивидуальных и групповых занятий в практике работы нейродефектолога»
- Диагностическая работа в образовательной организации в соответствии с ФГОС. Диагностика эмоционально-личностных особенностей детей
- Формирование познавательных универсальных учебных действий через использование современных образовательных технологий





